The origin of tablet boudinage: Results from experiments using power–law rock analogs. J. Zulauf , G. Zulauf, R. Kraus, G. Gutiérrez-Alonso, F. Zanella. 2011, Tectonophysics, 510, 327-336. DESCARGAR-DOWNLOAD
RESUMEN-ABSTRACT
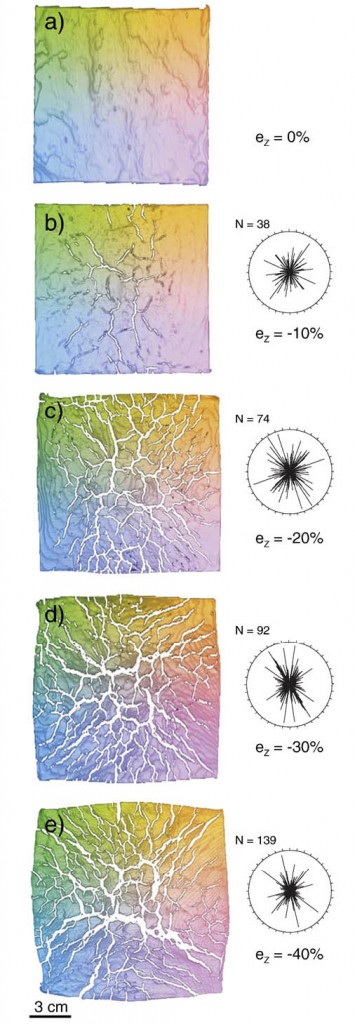
We used non-linear viscous plasticine as rock analogue to simulate boudinage of rocks undergoing dislocation creep and brittle fracture. A competent plasticine layer, oriented perpendicular to the main shortening direction, Z, underwent bulk pure flattening with equal layer-parallel extension in all directions inside a weaker plasticine matrix. The viscosity ratio between layer and matrix was set at 5 and the stress exponent of layer and matrix was 7. The samples were deformed at a strain rate, ė, of 5 * 10-5 s-1 up to a maximum finite strain, eZ, of -40%. Computer tomographic analyses of the deformed samples revealed that boudinage results from a first phase of viscous necking succeeded by extension fracture along the previously formed pinches. As the boudins display a polygonal shape in plan-view, they are referred to as ‘tablet boudins’ (in contrast to the rectangular chocolate-tablet boudins). The ratio between long and short axis, R, is ranging from 1.2 to 2.6 in plan-views. The polygonal, non-isometric shape of the tablet boudins is explained by the strong interaction of concentric and radial tensile fractures. With increasing layer thickness, Hi, the mean diameter of the boudins, Wa, increases, while the number of boudins, N, decreases. The relation between layer thickness and number of boudins can be described by the equation: N = A * exp(-Hi / B) + C, where A = 229 ±12, B = 0.89 ±0.04, and C = -0.2 ±1.0. Progressive finite strain results in a higher number and a smaller mean diameter of the boudins. The thickness of the boudins, Hf, is almost the same like the initial layer thickness, Hi, while the aspect ratio (Wd = Wa/Hf) decreases with layer thickness and finite strain. The mean Wd values obtained from all runs are ranging from ca. 4 to ca. 11. This range is higher than the values published so far for cylindrical and non-cylindrical boudins in the literature.